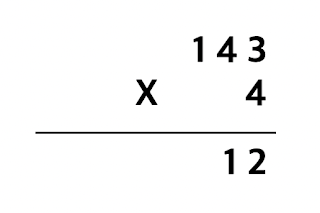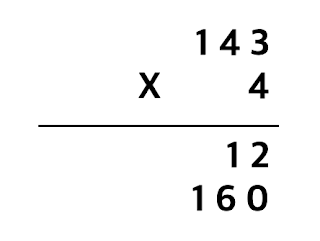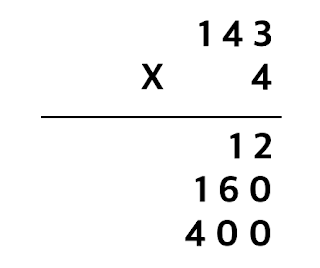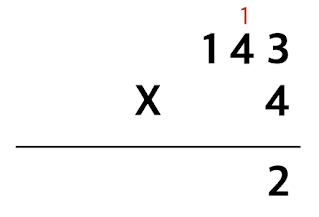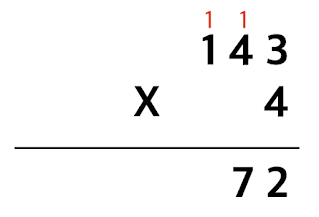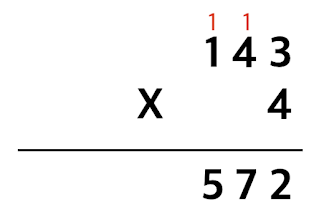올림이 있는 (세자리수) x (한 자리수) - 초등학교 3학년 수학
안녕하세요, 여러분! 지난 시간에는 받아올림이 없는 곱셈식을 푸는 법을 배웠죠. 오늘은 받아올림이 있는 자리수의 곱셈을 배워보겠습니다.
올림이 있는 (세자리수) x (한 자리수) - 초등학교 3학년 수학
예를 들어, "143 x 4"를 계산해야 한다고 가정해 봅시다. 이 문제를 이해하기 쉽게 하기 위해 다양한 방법으로 푸는 법을 알려드리겠습니다.
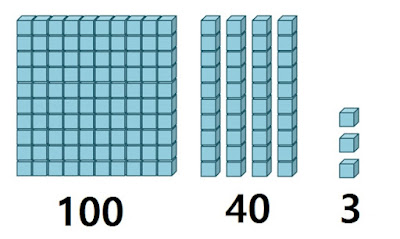
우선, 모형으로 알아보는 방법이 있습니다. 143을 모형으로 나타내면 백 모형이 4개, 십 모형이 16개, 일 모형이 3개입니다.
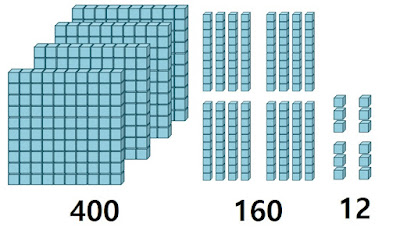
그러면 143 x 4는 143를 4번 더한 것과 같으므로, 백 모형 4개는 400, 십 모형 16개는 160, 일 모형 3개는 12입니다.
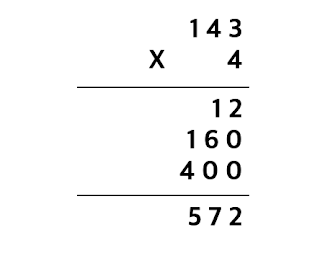
이 값을 모두 더하면 572가 됩니다. 그러므로, 143 x 4의 정답은 572입니다.
또한, 세로셈으로 알아보는 방법도 있습니다.
먼저 143 x 4를 세로셈으로 나타내어 일의 자리, 십의 자리, 백의 자리 순서로 곱셈을 하고, 그 결과를 자릿수를 맞춘 뒤에 모두 더합니다.
예를 들어, 일의 자리수인 3과 4를 곱하면 12가 되고, 이 때는 일의 자리인 2와 십의 자리인 1(받아올림)을 적어줍니다.
그리고, 십의 자리인 4와 4를 곱하면 16이 되는데, 받아올림이 있으므로 십의 자리에 10을 더해준 후, 그 결과인 7을 적어줍니다.
마지막으로 백의 자리인 1과 4를 곱하면 4가 되는데, 받아올림이 있으므로 백의 자리에 1을 더한 후, 5를 적어줍니다.
그러면, 계산 결과는 572가 됩니다.
<세로셈에서 받아올림 나타내기>
받아올림을 간단하게 나타내는 방법은, 세로셈을 더 쉽게 풀 수 있도록 도와주는 방법입니다. 예를 들어, "143 x 4"를 계산해야 한다고 가정해 봅시다.
이 문제를 세로셈으로 푸는 방법은 일의 자리, 십의 자리, 백의 자리 순서대로 곱셈을 하고, 그 결과를 자릿수를 맞춘 뒤에 모두 더하는 것입니다.
첫 번째 곱셈인 3 x 4의 결과는 12입니다. 이때 12의 일의 자리인 2는 아래에 적고, 십의 자리인 1은 올림 하여 적습니다.
그리고 두 번째 곱셈인 40 x 4의 결과는 160입니다. 이 때 160의 100은 백의 자리로 올림 하여 1을 적습니다. 그리고 60은 십의 자리에 올림 되어 있는 10과 더한 뒤, 아래에 십의 자리인 7만 적습니다.
마지막으로 100과 4를 곱한 결과는 400입니다. 그러나 100에 올림한 수가 있으므로, 400에 100을 더한 뒤, 500의 백의 자리인 5를 아래에 적습니다. 그러면, 계산 결과는 572가 됩니다.
학습지 미리보기
받아 올림이 있는 곱셈은, 올림이 없는 곱셈보다 계산이 조금 더 복잡해집니다. 이런 문제들은 높은 응용력을 요구하며, 개념적인 이해가 필요합니다.
느리더라도 개념부터 차근차근 쌓아 올리며 익숙해질 수 있도록 천천히 풀어보는 것이 좋습니다.